آدرس دهی باز. آدرس دهی باز یا درهم سازی بسته روشی برای حل تصادم در جدول درهم سازی است. در این روش با بررسی، یا جستجوی متناوب در میان خانه های آرایه تا زمانی که هدف یا یک خانه خالی بیابیم ادامه می یابد، رسیدن به خانهٔ خالی در جستجو برای یک کلید به معنای نبود این کلید در جدول می باشد. روش های شناخته شده برای ترتیب بررسی شامل موارد زیر است:
روشی که در آن ترتیب بررسی ثابت و معمولاً با قدم های به اندازه ۱ می باشد. اگر بخواهیم تابعی برای آن در نظر بگیریم به شکلی که i نشانگر تعداد دفعات حرکت جستجوگر برای یافتن کلید باشد و ( H1 ( k یک تابع درهم ساز باشد و m نشانگر تعداد خانه های جدول باشد، درهم ساز H را می توان به شکل زیر در نظر گرفت :
H ( k, i ) = ( H1 ( k ) +i ) mod m بررسی درجه دوم روشی که در آن ترتیب بررسی تابعی از درجه دوم می باشد، اگر H1 ( k ) , m , i را مانند بررسی خطی تعریف کنیم و a , b دو عدد دلخواه باشند برای بررسی درجه دوم تابعی مانند تابع زیر خواهیم داشت :
H ( k, i ) = ( H1 ( k ) +ai2+bi ) mod m درهم سازی مضاعف حالتی که توالی جستجو برای هر کلید ثابت است اما به وسیله یک درهم ساز دیگر محاسبه می شود. , اگر H1 ( k ) , m , i را مانند بررسی خطی تعریف کنیم و ( h2 ( k نیز یک تابع درهم ساز باشد برای درهم سازی مضاعف تابعی مانند تابع زیر خواهیم داشت :
H ( k, i ) = ( H1 ( k ) +iH2 ( k ) ) mod m در بررسی بین این سه روش، بررسی خطی بهترین عملکرد کش را دارد ولی وقوع تصادم در آن معمول تر است، درحالی که درهم سازی مضاعف عملکرد کش ضعیفی دارد ولی به طور تقریبی هیچ تصادمی در آن اتفاق نمی افتد و بررسی درجه دوم در ناحیه ای بین این دو حالت قرار می گیرد. همچنین درهم سازی مضاعف به محاسبه بیشتری نسبت به روش های دیگر نیاز دارد.
در تعدادی دیگر از روش های آدرس دهی باز، فرایند کلیدهای موجود در جدول را جابه جا کرده و یک خانهٔ خالی برای کلید جدید ایجاد می کنند. این روش ها حداکثر زمان جستجوی کمتری نسبت به روش های بر مبنای بررسی ( مانند روش های بالا ) ارائه می دهند.
یک عامل بحرانی در مورد درهم سازی های با آدرس دهی باز ضریب بار ( یا عامل بار ) است. باید توجه داشت که منظور از ضریب بار، نسبت تعداد خانه های پر جدول به تعداد کل خانه های جدول می باشد. هنگامی که ضریب بار افزایش می یابد و به ۱۰۰٪ نزدیک می شود، تعداد بررسی های مورد نیاز برای پیدا کردن یا درج یک کلید به شکل چشمگیری افزایش می یابد. هنگامی که جدول کاملاً پر می شود، ممکن است الگوریتم های بررسی نتوانند درست کار کنند. حتی با یک تابع درهم سازی خوب، معمولاً ضریب بار به ۸۰٪ محدود می شود. یک درهم ساز ضعیف حتی در حالی که بسیاری از جدول خالی است در نتیجه ضریب بار پایین است با تولید تعداد قابل توجهی تصادم کارایی بسیار پایینی نشان می دهد. [ درحال ویرایش]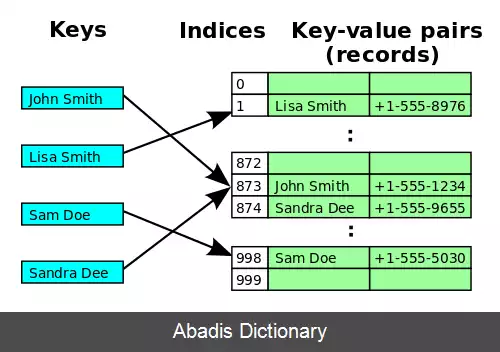
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفروشی که در آن ترتیب بررسی ثابت و معمولاً با قدم های به اندازه ۱ می باشد. اگر بخواهیم تابعی برای آن در نظر بگیریم به شکلی که i نشانگر تعداد دفعات حرکت جستجوگر برای یافتن کلید باشد و ( H1 ( k یک تابع درهم ساز باشد و m نشانگر تعداد خانه های جدول باشد، درهم ساز H را می توان به شکل زیر در نظر گرفت :
H ( k, i ) = ( H1 ( k ) +i ) mod m بررسی درجه دوم روشی که در آن ترتیب بررسی تابعی از درجه دوم می باشد، اگر H1 ( k ) , m , i را مانند بررسی خطی تعریف کنیم و a , b دو عدد دلخواه باشند برای بررسی درجه دوم تابعی مانند تابع زیر خواهیم داشت :
H ( k, i ) = ( H1 ( k ) +ai2+bi ) mod m درهم سازی مضاعف حالتی که توالی جستجو برای هر کلید ثابت است اما به وسیله یک درهم ساز دیگر محاسبه می شود. , اگر H1 ( k ) , m , i را مانند بررسی خطی تعریف کنیم و ( h2 ( k نیز یک تابع درهم ساز باشد برای درهم سازی مضاعف تابعی مانند تابع زیر خواهیم داشت :
H ( k, i ) = ( H1 ( k ) +iH2 ( k ) ) mod m در بررسی بین این سه روش، بررسی خطی بهترین عملکرد کش را دارد ولی وقوع تصادم در آن معمول تر است، درحالی که درهم سازی مضاعف عملکرد کش ضعیفی دارد ولی به طور تقریبی هیچ تصادمی در آن اتفاق نمی افتد و بررسی درجه دوم در ناحیه ای بین این دو حالت قرار می گیرد. همچنین درهم سازی مضاعف به محاسبه بیشتری نسبت به روش های دیگر نیاز دارد.
در تعدادی دیگر از روش های آدرس دهی باز، فرایند کلیدهای موجود در جدول را جابه جا کرده و یک خانهٔ خالی برای کلید جدید ایجاد می کنند. این روش ها حداکثر زمان جستجوی کمتری نسبت به روش های بر مبنای بررسی ( مانند روش های بالا ) ارائه می دهند.
یک عامل بحرانی در مورد درهم سازی های با آدرس دهی باز ضریب بار ( یا عامل بار ) است. باید توجه داشت که منظور از ضریب بار، نسبت تعداد خانه های پر جدول به تعداد کل خانه های جدول می باشد. هنگامی که ضریب بار افزایش می یابد و به ۱۰۰٪ نزدیک می شود، تعداد بررسی های مورد نیاز برای پیدا کردن یا درج یک کلید به شکل چشمگیری افزایش می یابد. هنگامی که جدول کاملاً پر می شود، ممکن است الگوریتم های بررسی نتوانند درست کار کنند. حتی با یک تابع درهم سازی خوب، معمولاً ضریب بار به ۸۰٪ محدود می شود. یک درهم ساز ضعیف حتی در حالی که بسیاری از جدول خالی است در نتیجه ضریب بار پایین است با تولید تعداد قابل توجهی تصادم کارایی بسیار پایینی نشان می دهد. [ درحال ویرایش]

wiki: آدرس دهی باز
