اثر بهمنی
فرهنگستان زبان و ادب
دانشنامه عمومی
اثر بهمنی، [ ۱] در رمزنگاری، خصلتی مطلوب در الگوریتم های رمزنگاری، معمولاً در رمزگذاری قطعه ای و تابع هش می باشد به طوری که یک تغییر کوچک ( نظیر تغییر یک بیت ) در ورودی منجر به تغییرات وسیع ( مثلاً تغییر نیمی از بیت ها ) در خروجی گردد. در مورد بلوک رمزهای با کیفیت بالا چنین تغییر کوچکی در کلید یا متن باید باعث تغییرات زیاد در متن رمزنگاری شده می گردد. اصطلاح اصلی نخستین بار توسط هورست فیستل مورد استفاده قرار گرفت ، اگرچه این مفهوم به حداقل انتشار شانون باز می گردد. تابع هش SHA - 1 اثر بهمنی را به خوبی نشان می دهد. وقتی یک بیت واحد تغییر می کند ، مقدار هش کاملاً متفاوت می شود.
اگر یک بلوک رمز یا تابع رمزنگاری هش دارای مقدار قابل توجهی اثر بهمنی نباشد، متن رمزنگاری شده به میزان کافی تصادفی نخواهد بود و در نتیجه یک تحلیلگر رمز قادر به پیش بینی ورودی های داده شده بر اساس خروجی خواهد بود. ممکن است همین نقص منجر به شکستن الگوریتم رمز به صورت ناقص یا کامل گردد. بنابراین ، اثر بهمنی از نظر طراح الگوریتم یا دستگاه رمزنگاری شرایط مطلوبی است.
ساخت یک الگوریتم رمز یا هش با قابلیت اثر بهمنی خوب یکی از اهداف اولیه و مهم می باشد که معمولاً در طراحی ریاضی آن از اثر پروانه ای استفاده می گردد. به همین دلیل است که اکثر بلوک های رمزگذاری متن رمز شده تولید می کنند. به همین دلیل است که توابع هش دارای بلوک داده های بزرگ هستند. هر دوی این ویژگی ها اجازه می دهند تا تغییرات کوچک در طول تکرار الگوریتم به سرعت پخش شوند ، به گونه ای که هر بیت خروجی باید قبل از خاتمه الگوریتم به هر بیت ورودی بستگی داشته باشد. . [ ۲] [ ۳]
معیاری رسمی و معین برای اثر بهمنی است. این معیار بیان می کند هر زمان که یک تک بیت ورودی تکمیل شود ، هر یک از بیت های خروجی با احتمال 50٪ تغییر می کند. SAC مبتنی بر مفاهیم تکامل و اثر بهمنی است و در سال 1985 توسط وبستر و تاورز معرفی شد.
مرتبه های بالاتر SAC شامل چند بیت ورودی است. توابع بولی که بالاترین مرتبه SAC را برآورده می کنند ، همیشه توابع خمیده هستند ، همچنین توابع "حداکثر غیرخطی" و نیز توابع "کامل غیرخطی" نامیده می شوند.
BIC بیان می کند که وقتی هر بیت ورودی i به ازای همه i ، j و k معکوس ( invert ) شود؛ بیت های خروجی j و k باید بطور مستقل تغییر کنند.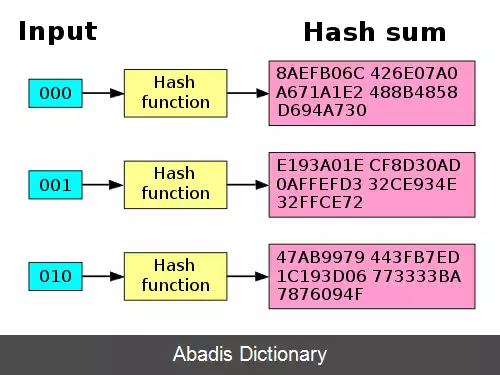
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفاگر یک بلوک رمز یا تابع رمزنگاری هش دارای مقدار قابل توجهی اثر بهمنی نباشد، متن رمزنگاری شده به میزان کافی تصادفی نخواهد بود و در نتیجه یک تحلیلگر رمز قادر به پیش بینی ورودی های داده شده بر اساس خروجی خواهد بود. ممکن است همین نقص منجر به شکستن الگوریتم رمز به صورت ناقص یا کامل گردد. بنابراین ، اثر بهمنی از نظر طراح الگوریتم یا دستگاه رمزنگاری شرایط مطلوبی است.
ساخت یک الگوریتم رمز یا هش با قابلیت اثر بهمنی خوب یکی از اهداف اولیه و مهم می باشد که معمولاً در طراحی ریاضی آن از اثر پروانه ای استفاده می گردد. به همین دلیل است که اکثر بلوک های رمزگذاری متن رمز شده تولید می کنند. به همین دلیل است که توابع هش دارای بلوک داده های بزرگ هستند. هر دوی این ویژگی ها اجازه می دهند تا تغییرات کوچک در طول تکرار الگوریتم به سرعت پخش شوند ، به گونه ای که هر بیت خروجی باید قبل از خاتمه الگوریتم به هر بیت ورودی بستگی داشته باشد. . [ ۲] [ ۳]
معیاری رسمی و معین برای اثر بهمنی است. این معیار بیان می کند هر زمان که یک تک بیت ورودی تکمیل شود ، هر یک از بیت های خروجی با احتمال 50٪ تغییر می کند. SAC مبتنی بر مفاهیم تکامل و اثر بهمنی است و در سال 1985 توسط وبستر و تاورز معرفی شد.
مرتبه های بالاتر SAC شامل چند بیت ورودی است. توابع بولی که بالاترین مرتبه SAC را برآورده می کنند ، همیشه توابع خمیده هستند ، همچنین توابع "حداکثر غیرخطی" و نیز توابع "کامل غیرخطی" نامیده می شوند.
BIC بیان می کند که وقتی هر بیت ورودی i به ازای همه i ، j و k معکوس ( invert ) شود؛ بیت های خروجی j و k باید بطور مستقل تغییر کنند.

wiki: اثر بهمنی
پیشنهاد کاربران
پیشنهادی ثبت نشده است. شما اولین نفر باشید
