اتوماتون بوچی ( زبان انگلیسی: Büchi automaton ) را می توان به عنوان اتوماتونی در نظر گرفت که می توانند رشته های نامتناهی الفبا را بپذیرد. این اتوماتون اولین بار توسط ژولیوس ریچارد بوچی ( Julius Richard Büchi ) منطق دان سوئیسی در سال ۱۹۶۲ معرفی شد. [ ۱] اگر ω را به عنوان مجموعه اعداد طبیعی و Σ رابه عنوان الفبا در نظر بگیریم یک کلمه نامتناهی ( یا یک ω - کلمه ) را می توان به عنوان یک تابع از ω به Σ در نظر گرفت به این ترتیب مجموعه تمام کلمه های نامتناهی را با Σ ω نشان می دهیم.
یک اتوماتون بوچی قطعی ۵ تایی A = ( Q , Σ , δ , q 0 , F ) است که در ان:
• Q مجموعه ای محدود از حالات است.
• Σ مجموعه ای محدود از نمادها است که الفبای A یا الفبای ورودی خوانده می شود.
• δ : Q × Σ → Q {\displaystyle \delta :Q\times \Sigma \rightarrow Q} تابع انتقال است.
• q 0 {\displaystyle q_{0}} عضوی از Q است و حالت ابتدایی نامیده می شود
• F ⊂ Q {\displaystyle F\subset Q} مجموعه حالات قبول یا پایانی خوانده می شود.
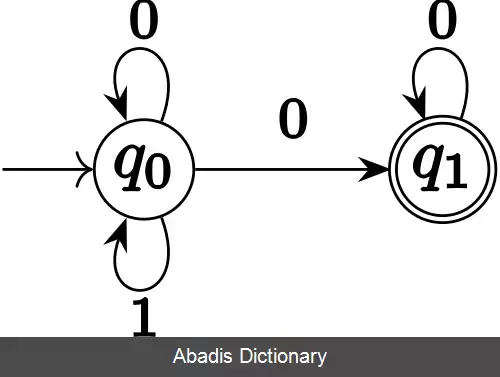
فرض کنید A = ( Q , Σ , δ , q 0 , F ) یک اتوماتون بوچی متناهی باشد در این صورت یک تعمیم طبیعی از مفهوم اجرا ( نسبت به اتوماتون قطعی متناهی ) می تواند مطرح شود که به این صورت است که یک اجرا روی یک کلمه نامتناهی σ = a 1 a 2 a 3 . . . را به صورت دنبالهٔ r = s q 1 q 2 q 3 . . . تعریف می کنیم که از s شروع می کنیم و با a 1 به q 1 و سپس با a 2 به q 2 و… می رویم. به عنوان مثال در این اتوماتون:
اگر σ = 100 ω . . در اینصورت r = q 0 q 1 q 1 ω یه اجرای A است.
در این صورت می گوییم ماشین A رشته σ را قبول می کند اگر اجرایی وجود داشته باشد که در ان حداقل یکی از حالات قبول را به تعداد نامتناهی دیده باشیم.
در اتوماتون بوچی غیرقطعی به جای تابع انتقال، رابطهٔ انتفال مطرح است و مانند NFA هر حالت تحت رابطهٔ انتقال به مجموعه ای از حالات منجر می شود و به جای حالت آغازی مجموعه از حالات ابتدایی در نظر گرفته می شود. در حالت کلی وقتی کلمه اتوماتون بوچی را به تنهایی به کار می بریم منظورمان اتوماتون بوچی غیرقطعی است.
مجموعه تمام ω - کلمه های را که یک بوچی اتوماتون قبول می کند زبان ان بوچی اتوماتون می گویند. حالا یک زبان A ⊂ Σ ω را بوچی تشخیص پذیر می گوییم اگر بوچی اتوماتون M ای پیدا شود که L ( M ) = A . یک زبان بوچی تشخیص پذیر است اگر و فقط اگر یک زبان امگا ی منظم باشد. مثلاً A = Σ ∗ a ω ⋃ Σ ∗ ( a b ) ω .
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفیک اتوماتون بوچی قطعی ۵ تایی A = ( Q , Σ , δ , q 0 , F ) است که در ان:
• Q مجموعه ای محدود از حالات است.
• Σ مجموعه ای محدود از نمادها است که الفبای A یا الفبای ورودی خوانده می شود.
• δ : Q × Σ → Q {\displaystyle \delta :Q\times \Sigma \rightarrow Q} تابع انتقال است.
• q 0 {\displaystyle q_{0}} عضوی از Q است و حالت ابتدایی نامیده می شود
• F ⊂ Q {\displaystyle F\subset Q} مجموعه حالات قبول یا پایانی خوانده می شود.
فرض کنید A = ( Q , Σ , δ , q 0 , F ) یک اتوماتون بوچی متناهی باشد در این صورت یک تعمیم طبیعی از مفهوم اجرا ( نسبت به اتوماتون قطعی متناهی ) می تواند مطرح شود که به این صورت است که یک اجرا روی یک کلمه نامتناهی σ = a 1 a 2 a 3 . . . را به صورت دنبالهٔ r = s q 1 q 2 q 3 . . . تعریف می کنیم که از s شروع می کنیم و با a 1 به q 1 و سپس با a 2 به q 2 و… می رویم. به عنوان مثال در این اتوماتون:
اگر σ = 100 ω . . در اینصورت r = q 0 q 1 q 1 ω یه اجرای A است.
در این صورت می گوییم ماشین A رشته σ را قبول می کند اگر اجرایی وجود داشته باشد که در ان حداقل یکی از حالات قبول را به تعداد نامتناهی دیده باشیم.
در اتوماتون بوچی غیرقطعی به جای تابع انتقال، رابطهٔ انتفال مطرح است و مانند NFA هر حالت تحت رابطهٔ انتقال به مجموعه ای از حالات منجر می شود و به جای حالت آغازی مجموعه از حالات ابتدایی در نظر گرفته می شود. در حالت کلی وقتی کلمه اتوماتون بوچی را به تنهایی به کار می بریم منظورمان اتوماتون بوچی غیرقطعی است.
مجموعه تمام ω - کلمه های را که یک بوچی اتوماتون قبول می کند زبان ان بوچی اتوماتون می گویند. حالا یک زبان A ⊂ Σ ω را بوچی تشخیص پذیر می گوییم اگر بوچی اتوماتون M ای پیدا شود که L ( M ) = A . یک زبان بوچی تشخیص پذیر است اگر و فقط اگر یک زبان امگا ی منظم باشد. مثلاً A = Σ ∗ a ω ⋃ Σ ∗ ( a b ) ω .


wiki: اتوماتون بوچی
