در محاسبات کوانتومی، اتوماتای متناهی کوانتومی ( quantum finite automata ) یا ( QFA ) یا ماشین های حالت کوانتومی ( quantum state machines ) ، حالتی کوانتومی از اتوماتای احتمالاتی یا یک فرایند تصمیم مارکوف می باشد. انواع مختلفی از اتومات ها همانند measure - once و measure - many تعریف شده اند. در واقع اتوماتای متناهی کوانتومی نمونه خاصی از اتوماتای متناهی هندسی و اتوماتای متناهی توپولوژیکی می باشد.
اتوماتا با پذیرش یک رشته به طول متناهی σ = ( σ 0 , σ 1 , ⋯ , σ k ) از σ i ها از یک الفبای ورودی Σ و اختصاص احتمال Pr ( σ ) به هر رشته کار خواهد کرد. این احتمال بیانگر قرارگیری احتمال اتوماتون در حالت پذیرش می باشد، اینکه رشته پذیرفته می شود یا خیر.
زبان های پذیرفته شده QFA نه زبان های معمول اتوماتای متناهی قطعی هست و نه زبان تصادفی اتوماتای متناهی احتمالاتی. در واقع مطالعه زبان های کوانتوم همواره بخش مناسبی برای تحقیقات علمی بوده است.
راهی ساده و شهودی برای دریافت درکی صحیح از اتوماتای متناهی کوانتومی وجود دارد که شروع آن از طریق تفسیر اتوماتای متناهی قطعی ( DFA ) به کمک نظریه گراف امکان پذیر می شود. یک DFA را می توان یک گراف جهت دار، حالات را راس گراف و یال های جهت دار را انتقال دهنده های حالت در نظر گرفت. هر یال جهت دار با نماد ورودی ممکن برچسب گذاری می شود؛ بنابراین دادن یک نماد مشخص و حالت مشخص به یال های جهت دار قدم بعدی می باشد. یکی از راه های معرفی همچین گرافی به کمک ماتریس های مجاورت امکان پذیر است به این صورت که برای هر نماد ورودی یک ماتریس در نظر گرفته شود. در این مورد، لیست حالت های ممکن DFA به صورت یک بردار ستونی نوشته می شود. با دادن یک نماد ورودی ماتریس مجاورت نشان خواهد داد که چگونه دادن هر ( سطر در بردار حالت ) به حالت بعدی انتقال خواهد یافت. یک انتقال حالت با ضرب ماتریس ها صورت می گیرد.
هر عنصر ورودی، عامل انتقال متفاوتی می باشد بنابراین نیاز به یک ماتریس مجاورت متمایز برای هر نماد ورودی ممکن است. درایه های این ماتریس می بایست همگی صفر و یک باشند. برای هر ستون ماتریس فقط یک درایه ناصفر وجود دارد که این درایه نشان دهنده انتقال حالت منحصر به فرد بعدی می باشد. به طور مشابه، حالت سیستم، یک بردار ستونی است که فقط دارای یک درایه ناصفر می باشد که این درایه مطابق حالت فعلی سیستم است. فرض کنید Σ = { α } به عنوان مجموعه ای از نمادهای ورودی باشد. برای هر α ∈ Σ ، U α را به عنوان ماتریس مجاورت داریم که نشان دهنده سیر تکامل DFA به حالت بعدی خودش هست؛ بنابراین مجموعه { U α | α ∈ Σ } به طور کامل انتقال حالت عملگر DFA را شرح می دهد. فرض کنید Q مجموعه حالت های ممکن از DFA باشد. اگر N حالت در Q وجود داشته باشد آنگاه هر ماتریس U α ، N با N - بعد خواهد بود. حالت شروع q 0 ∈ Q مطابق یک بردار ستونی با یک ۱ در سطر q0ام می باشد. حالت عمومیq وقتی است که یک بردار ستونی با یک ۱ در سطر qام باشد. با تخطی از نشانه گذاری معمول، فرض کنید q0 و q دوبردار باشند. سپس، بعد از خواندن نمادهای ورودی α β γ ⋯ از نوار ورودی حالت DFA طبق q = ⋯ U γ U β U α q 0 . مشخص خواهد شد. انتقال حالت توسط ضرب ماتریس ها صورت می گیرد ( مثلاً ضرب q0 با U α ، یا غیره ) .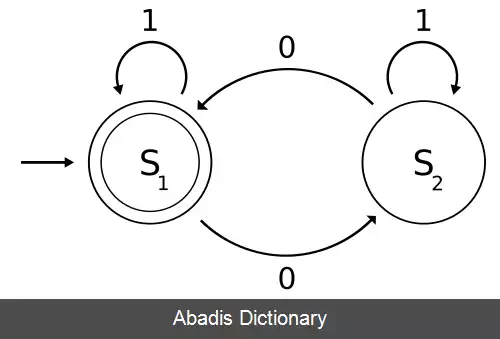
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفاتوماتا با پذیرش یک رشته به طول متناهی σ = ( σ 0 , σ 1 , ⋯ , σ k ) از σ i ها از یک الفبای ورودی Σ و اختصاص احتمال Pr ( σ ) به هر رشته کار خواهد کرد. این احتمال بیانگر قرارگیری احتمال اتوماتون در حالت پذیرش می باشد، اینکه رشته پذیرفته می شود یا خیر.
زبان های پذیرفته شده QFA نه زبان های معمول اتوماتای متناهی قطعی هست و نه زبان تصادفی اتوماتای متناهی احتمالاتی. در واقع مطالعه زبان های کوانتوم همواره بخش مناسبی برای تحقیقات علمی بوده است.
راهی ساده و شهودی برای دریافت درکی صحیح از اتوماتای متناهی کوانتومی وجود دارد که شروع آن از طریق تفسیر اتوماتای متناهی قطعی ( DFA ) به کمک نظریه گراف امکان پذیر می شود. یک DFA را می توان یک گراف جهت دار، حالات را راس گراف و یال های جهت دار را انتقال دهنده های حالت در نظر گرفت. هر یال جهت دار با نماد ورودی ممکن برچسب گذاری می شود؛ بنابراین دادن یک نماد مشخص و حالت مشخص به یال های جهت دار قدم بعدی می باشد. یکی از راه های معرفی همچین گرافی به کمک ماتریس های مجاورت امکان پذیر است به این صورت که برای هر نماد ورودی یک ماتریس در نظر گرفته شود. در این مورد، لیست حالت های ممکن DFA به صورت یک بردار ستونی نوشته می شود. با دادن یک نماد ورودی ماتریس مجاورت نشان خواهد داد که چگونه دادن هر ( سطر در بردار حالت ) به حالت بعدی انتقال خواهد یافت. یک انتقال حالت با ضرب ماتریس ها صورت می گیرد.
هر عنصر ورودی، عامل انتقال متفاوتی می باشد بنابراین نیاز به یک ماتریس مجاورت متمایز برای هر نماد ورودی ممکن است. درایه های این ماتریس می بایست همگی صفر و یک باشند. برای هر ستون ماتریس فقط یک درایه ناصفر وجود دارد که این درایه نشان دهنده انتقال حالت منحصر به فرد بعدی می باشد. به طور مشابه، حالت سیستم، یک بردار ستونی است که فقط دارای یک درایه ناصفر می باشد که این درایه مطابق حالت فعلی سیستم است. فرض کنید Σ = { α } به عنوان مجموعه ای از نمادهای ورودی باشد. برای هر α ∈ Σ ، U α را به عنوان ماتریس مجاورت داریم که نشان دهنده سیر تکامل DFA به حالت بعدی خودش هست؛ بنابراین مجموعه { U α | α ∈ Σ } به طور کامل انتقال حالت عملگر DFA را شرح می دهد. فرض کنید Q مجموعه حالت های ممکن از DFA باشد. اگر N حالت در Q وجود داشته باشد آنگاه هر ماتریس U α ، N با N - بعد خواهد بود. حالت شروع q 0 ∈ Q مطابق یک بردار ستونی با یک ۱ در سطر q0ام می باشد. حالت عمومیq وقتی است که یک بردار ستونی با یک ۱ در سطر qام باشد. با تخطی از نشانه گذاری معمول، فرض کنید q0 و q دوبردار باشند. سپس، بعد از خواندن نمادهای ورودی α β γ ⋯ از نوار ورودی حالت DFA طبق q = ⋯ U γ U β U α q 0 . مشخص خواهد شد. انتقال حالت توسط ضرب ماتریس ها صورت می گیرد ( مثلاً ضرب q0 با U α ، یا غیره ) .

wiki: اتوماتای متناهی کوانتومی
