K برش کمینه. در ریاضیات، مسئلهٔ حداقل k برش، یک مسئلهٔ بهینه سازی ترکیبیاتی است که به یافتن یک مجموعه از یال ها اشاره دارد که حذف این مجموعه، گراف را به حداقل k مولفهٔ همبندی تقسیم بندی کند. به این یال ها k - برش گفته می شود و به یالی که حذف آن باعث افزایش مولفه های همبندی شود پل ( نظریه گراف ) گفته می شود. این مسئله زیرمجموعه و مشتق شدهٔ مسئلهٔ حداقل برش است که کارکرد جزئی تری نسبت به مسئله اصلی دارد. هدف یافتن k - برش با وزن کمینه است. این تقسیم بندی می تواند کاربردهایی در طراحی وی ال اس آی، داده کاوی، روش اجزاء محدود و ارتباطات در رایانش موازی داشته باشد.
گراف بدون جهت G = ( E, V ) و عدد k ∈ {۲, ۳, …, |V|} داده شده است. به هر یال گراف G یک وزن w: E → N اختصاص یافته است. V را به k مجموعه جدا تقسیم بندی کنید در حالی که عبارت زیر کمینه شود
برای k ثابت، این مسئله، مسئله زمان چند جمله ای است که در O ( |V|k2 ) قابل حل است. [ ۱] با این حال، اگر k بخشی از ورودی باشد، مسئله به یک مسئلهٔ NP کامل است. [ ۲] در صورتی که ما k رأس را مشخص کنیم و کمترین k برش برای جدا کردن این k رأس را بخواهیم این مسئله بازهم یک مسئلهٔ NP کامل خواهد شد. [ ۳]
کمترین برش هنگامی اهمیت پیدا می کند که گرافی بسیار بزرگ در اختیار داشته باشیم و بخواهیم آن را مورد بررسی قرار دهیم. در این حالت بررسی کل گراف به صورت کلی کاربردی نخواهد بود و ما در تلاشیم با تقسیم گراف به صورت معقول و عملی هزینه اجرای الگوریتم های گراف را بر روی تمام داده های خود بهینه کنیم. با تقسیم گراف به مؤلفه های همبندی، اصطلاحاً تعدادی تکه شکسته خواهیم داشت که به معنای سهولت قراردهی داده ها در سرورهای مختلف خواهد بود.
مسئلهٔ k برش کمینه در حوزه های متنوعی که موضوع شبکه مطرح می شود، کاربرد دارد، به عنوان مثال از آن برای تقسیم بندی گروه های علاقه مندی در شبکه های اجتماعی یا برای یافتن ضعیف ترین اتصالات در شبکه های مخابراتی یا در یافتن خلوت ترین معابر در شبکه های ترافیکی استفاده می شود.
چندین الگوریتم تقریبی با تقریب 2 - 2/k وجود دارد. یک الگوریتم حریصانه ساده با این عامل تقریبی این است که حداقل برش در هر یک از اجزای متصل ( مؤلفه همبندی ) را محاسبه می کند و سنگین ترین را حذف می کند. این الگوریتم به طور کلی به n - 1 بار محاسبه بیشینه جریان دارد. الگوریتم دیگری برای دستیابی به همان تقریب از نمای درخت گوموری هو از حداقل برش ها استفاده می کند. ساخت درخت گوموری هو به n - 1 بار محاسبه جریان بیشینه احتیاج دارد که الگوریتم آن با محاسبه کلی بیشینه جریان از O ( kn ( انجام می دهد. با این حال، تجزیه و تحلیل عامل تقریب الگوریتم دوم آسان تر است. [ ۴] [ ۵] علاوه بر این، تحت فرضیه گسترش مجموعه کوچک ( حدسی بسیار مرتبط با حدس بازی منحصر به فرد ) ، مسئله تقریباً نزدیک به NP است با عامل ( 2 − ϵ ) برای هر ثابت ϵ > 0 . [ ۶] این به معنای آن است که الگوریتم های تقریبی فوق الذکر در اصل برای kهای بزرگ به جواب اصلی نزدیک تر هستند.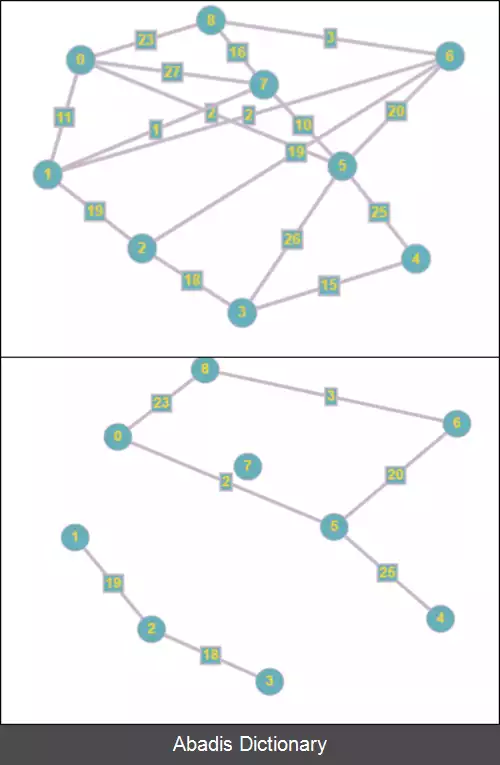
این نوشته برگرفته از سایت ویکی پدیا می باشد، اگر نادرست یا توهین آمیز است، لطفا گزارش دهید: گزارش تخلفگراف بدون جهت G = ( E, V ) و عدد k ∈ {۲, ۳, …, |V|} داده شده است. به هر یال گراف G یک وزن w: E → N اختصاص یافته است. V را به k مجموعه جدا تقسیم بندی کنید در حالی که عبارت زیر کمینه شود
برای k ثابت، این مسئله، مسئله زمان چند جمله ای است که در O ( |V|k2 ) قابل حل است. [ ۱] با این حال، اگر k بخشی از ورودی باشد، مسئله به یک مسئلهٔ NP کامل است. [ ۲] در صورتی که ما k رأس را مشخص کنیم و کمترین k برش برای جدا کردن این k رأس را بخواهیم این مسئله بازهم یک مسئلهٔ NP کامل خواهد شد. [ ۳]
کمترین برش هنگامی اهمیت پیدا می کند که گرافی بسیار بزرگ در اختیار داشته باشیم و بخواهیم آن را مورد بررسی قرار دهیم. در این حالت بررسی کل گراف به صورت کلی کاربردی نخواهد بود و ما در تلاشیم با تقسیم گراف به صورت معقول و عملی هزینه اجرای الگوریتم های گراف را بر روی تمام داده های خود بهینه کنیم. با تقسیم گراف به مؤلفه های همبندی، اصطلاحاً تعدادی تکه شکسته خواهیم داشت که به معنای سهولت قراردهی داده ها در سرورهای مختلف خواهد بود.
مسئلهٔ k برش کمینه در حوزه های متنوعی که موضوع شبکه مطرح می شود، کاربرد دارد، به عنوان مثال از آن برای تقسیم بندی گروه های علاقه مندی در شبکه های اجتماعی یا برای یافتن ضعیف ترین اتصالات در شبکه های مخابراتی یا در یافتن خلوت ترین معابر در شبکه های ترافیکی استفاده می شود.
چندین الگوریتم تقریبی با تقریب 2 - 2/k وجود دارد. یک الگوریتم حریصانه ساده با این عامل تقریبی این است که حداقل برش در هر یک از اجزای متصل ( مؤلفه همبندی ) را محاسبه می کند و سنگین ترین را حذف می کند. این الگوریتم به طور کلی به n - 1 بار محاسبه بیشینه جریان دارد. الگوریتم دیگری برای دستیابی به همان تقریب از نمای درخت گوموری هو از حداقل برش ها استفاده می کند. ساخت درخت گوموری هو به n - 1 بار محاسبه جریان بیشینه احتیاج دارد که الگوریتم آن با محاسبه کلی بیشینه جریان از O ( kn ( انجام می دهد. با این حال، تجزیه و تحلیل عامل تقریب الگوریتم دوم آسان تر است. [ ۴] [ ۵] علاوه بر این، تحت فرضیه گسترش مجموعه کوچک ( حدسی بسیار مرتبط با حدس بازی منحصر به فرد ) ، مسئله تقریباً نزدیک به NP است با عامل ( 2 − ϵ ) برای هر ثابت ϵ > 0 . [ ۶] این به معنای آن است که الگوریتم های تقریبی فوق الذکر در اصل برای kهای بزرگ به جواب اصلی نزدیک تر هستند.

wiki: K برش کمینه
